Resolución de
Problemas
Matematización
La evaluación SIMCE estudia la capacidad de los
alumnos para analizar, razonar y comunicar ideas matemáticas de forma efectiva
al plantear, resolver e interpretar problemas matemáticos en distintas
situaciones. La solución de problemas requiere que los alumnos hagan uso de las
habilidades y competencias que han adquirido a lo largo de su escolarización y
a través de sus propias experiencias vitales. Este proceso fundamental que
emplean los alumnos para resolver los problemas que plantea la vida real se denomina
matematización.
En el apartado que se ocupaba de las
bases teóricas del marco PISA de evaluación de las matemáticas se esbozaba una
descripción de las matemáticas en cinco pasos. En la Figura 3.8 se recogen esos
pasos, que aparecen luego en forma de lista.
Se inicia con un problema situado en la
realidad.
• Se organiza de acuerdo
con conceptos matemáticos y se identifican las matemáticas relevantes al caso.
• El problema se va
abstrayendo progresivamente de la realidad mediante una serie de procesos, como
la elaboración de supuestos, la generalización y la formalización, mediante los
cuales se destacan los rasgos matemáticos de la situación y se transforma el
problema del mundo real en un problema matemático que reproduce de manera fiel
la situación.
• Se resuelve el
problema matemático.
• Se confiere sentido a
la solución matemática en términos de la situación real, a la vez que se
identifican las posibles limitaciones de la solución.
La matematización comporta, en primer
lugar, la traducción del problema real a términos matemáticos.
Este proceso incluye diversas
operaciones, como por ejemplo:
• Identificar los
elementos matemáticos pertinentes al problema situado en la realidad.
• Representar el
problema de una manera distinta; lo cual comporta, entre otras cosas,
organizarlo de acuerdo con los conceptos matemáticos pertinentes y plantear los
supuestos adecuados al caso.
• Comprender las
relaciones existentes entre el lenguaje del problema y el lenguaje formal y
simbólico que se necesita para comprenderlo en términos matemáticos.
• Encontrar
regularidades, relaciones y patrones.
• Reconocer los aspectos
que son isomórficos respecto de otros problemas conocidos.
• Traducir el problema a
términos matemáticos, es decir, a un modelo matemático (de Lange, 1987).
Una vez que el alumno ha traducido el
problema a una forma matemática, el proceso puede continuarse ya dentro de un
ámbito estrictamente matemático. Los alumnos se plantearán preguntas del tipo:
«¿Hay...?» «En tal caso, ¿cuántos?» o «¿Cómo puedo hallar...?», recurriendo a
las habilidades y conceptos matemáticos de que dispone. Tratarán de desarrollar
el modelo del problema, adaptarlo, establecer regularidades, identificar
conexiones y crear una buena argumentación matemática.
Esta parte del proceso de matematización
suele conocerse como la parte deductiva del ciclo de construcción de modelos
(Blum, 1996; Schupp, 1988). Conviene señalar, no obstante, que en esta fase
pueden intervenir también otros procesos aparte del deductivo. Esta parte del
proceso de matematización comporta:
• Utilizar diferentes
tipos de representación e ir alternando entre ellos.
• Utilizar operaciones y
un lenguaje simbólico, formal y técnico.
• Refinar y ajustar los
modelos matemáticos mediante un proceso de combinación e integración de
modelos.
• Argumentar.
• Generalizar.
El último, o los últimos pasos, que han
de darse para resolver el problema implican una reflexión sobre el proceso en
su conjunto y sobre los resultados obtenidos. Llegados a este punto, los
alumnos deben interpretar los resultados con espíritu crítico y validar la
totalidad del proceso. Esta reflexión se da en todas las fases
del proceso, pero tiene especial importancia en esta fase final. Algunos de los
aspectos de este proceso de reflexión y validación son:
• La comprensión del
alcance y los límites de los conceptos matemáticos.
• La reflexión sobre las
argumentaciones matemáticas y la explicación y justificación de los resultados
obtenidos.
• La comunicación del
proceso y la solución.
• La crítica del modelo
y de sus límites.
Esta fase aparece indicada en dos puntos
de la Figura 3.8 mediante la referencia «5», que señala el momento del proceso
de matematización en que se pasa de la solución matemática a la solución real y
el momento en que esta última se relaciona de nuevo con el problema del mundo
real.
Proceso de Matematización aplicado en un
problema
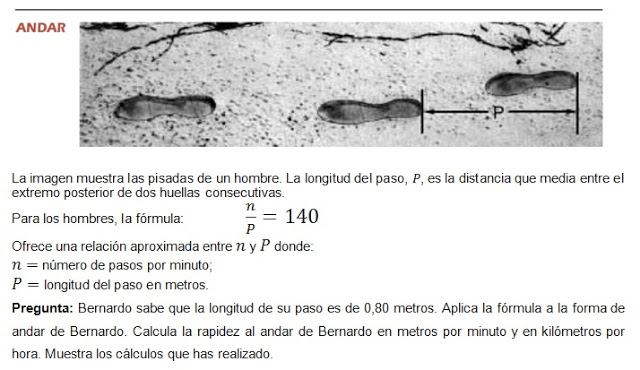
Problema: “Andar”
Fuente: © OCDE 2004 Informe
PISA 2003. Aprender para el mundo del mañana, pág 64.
Eje Temático: Números
y Álgebra
Grupo de Competencias: Conexión
Nivel de dificultad: Avanzado
Solución – Aunando
criterios mediante un método de resolución de problemas – Parte 1
La primera estructura
mental que debe plantear un estudiante es la siguiente:
Puede trazar al principio una línea punteada
subdividiendo el espacio para desarrollar el problema, se recomienda que
después la subdivisión sea imaginaria.
Luego es importante que
el docente guíe el proceso para que el estudiante comience por leer el problema
e identificar los datos importantes y reconocer la pregunta. Luego dibujar
esquemas o diagramas que permitan una mejor comprensión (cuando sea necesario),
plantear y resolver las ecuaciones correspondientes para finalmente redactar la
solución del problema guiándose por la pregunta y los resultados de los
ejercicios realizados:
Es recomendable, además, siempre durante el proceso
dejar claro que habilidades se pretende desarrollar, por lo que durante el
apoyo personalizado, el docente mediante preguntas dirigidas, debe hacer que
los jóvenes las mencionen con respuestas verbales.
Solución – Aunando
criterios mediante un método de resolución de problemas – Parte 2
Observaciones:
“Esta pregunta de respuesta abierta se sitúa en el contexto personal. La guía de codificación de esta pregunta prevé una
puntuación completa y dos niveles de puntuación parcial. La pregunta trata de
la relación entre el número de pasos por minuto y la longitud del paso.
Pertenece al área de contenido de cambio y relaciones. La rutina matemática necesaria para resolver el
problema con éxito consiste en la sustitución de una simple fórmula (álgebra) y
la realización de unos cálculos no rutinarios. Para resolver el problema, los
alumnos deben calcular primero el número de pasos por minuto cuando se da la
longitud del paso (0,8 m). Ello requiere la sustitución y el manejo de la
expresión: n/0,8 = 140 que lleva a: n =
140x0,8, que es 112 pasos por minuto. La siguiente pregunta pide la velocidad
en m/minuto que implica convertir el número de pasos en una distancia en
metros:112x0,80 = 89,6 metros; de modo que la velocidad del hombre en cuestión
es de 89,6 m/minuto.
El último paso consiste en transformar esta velocidad
en km/h, una unidad de velocidad de uso más común. Esto hace referencia a las
relaciones entre unidades de conversión, que forman parte de la competencia de la medición. Resolver el problema requiere también la decodificación e interpretación de un lenguaje
simbólico básico y el manejo de expresiones que contienen
símbolos y fórmulas. El problema,
por tanto, es bastante complejo,
ya que incluye la expresión algebraica formal y la realización de una secuencia
de cálculos distintos, pero conectados, que requieren la comprensión o la
transformación de fórmulas y unidades de medida. El nivel más bajo de
puntuación parcial de esta pregunta corresponde al grupo de competencias de conexión. El nivel más alto de puntuación parcial ilustra la
parte superior del nivel 5, con una dificultad de 666 puntos. Los alumnos que
alcanzan el nivel superior de puntuación parcial demuestran ser capaces de ir
más allá de encontrar el número de pasos por minuto, avanzando hacia la conversión
de esta cifra en una unidad de medida más estándar, como la que se les pide.
Sin embargo, sus respuestas no son del todo correctas o completas. La
puntuación máxima de esta pregunta ilustra la parte superior del nivel 6, ya
que tiene una dificultad de 723 puntos. Los alumnos que obtienen la puntuación
máxima son capaces de completar las conversiones y dar una respuesta correcta
en las dos unidades de medida requeridas”.
Anexo: TAXONOMÍA REVISADA DE BLOOM (2000)
"En los años 90, un antiguo estudiante de Bloom,
Lorin Anderson y David R. Krathwohl, revisaron la Taxonomía de su maestro y
la publicaron en diciembre de 2000. Uno de los aspectos clave
de esta revisión es el cambio de los sustantivos de la propuesta original a
verbos, para significar las acciones correspondientes a cada categoría. Otro
aspecto fue considerar la síntesis con un criterio más amplio y relacionarla
con crear (considerando que toda síntesis es en si misma una creación); además,
se modificó la secuencia en que se presentan las distintas categorías. A
continuación se presentan las categorías en orden ascendente, de inferior
a superior y se ilustran con la siguiente imagen:"
Referencias:
¡¡¡Buena suerte y no olviden dejar sus comentarios!!!







No hay comentarios:
Publicar un comentario